알고리즘의 시간복잡도,공간복잡도 를 나타낸다.
* 참고로 알고리즘의 복잡도는 시간복잡도와 공간복잡도가 있다.
시간복잡도
소스코드의 실행 시간을 예측하여 얼마나 효율적인지 나타낸다. 실행 시간은 연산에 비례한다.
공간복잡도
코드가 메모리공간을 얼마나 효율적으로 쓰는지를 나타낸다. 공간을 미리 확보해야하는 자료구조에 쓰인다.
시간복잡도의 세가지 표기법
- Big-O(빅-오) : 최악의 경우
- Big-Ω(빅-오메가) : 최선의 경우
- Big-θ(빅-세타) : 평균의 경우
이중 우리는 최악의 경우를 생각하여 알고리즘의 시간 복잡도를 나타낸다. 최선의 경우와 최악의 경우가 차이가 많이 나는 경우도 있기 때문.
빅오 표기법의 종류
1. O(1) Constant
입력값이 아무리 커도 실행 시간은 일정하다.
ex ) 해시테이블의 조회, 삽입
2. O(log₂ n) Logarithmic
실행 시간이 입력 값에 영향을 받는 경우이다. 하지만 log값이므로 크게 영향을 받지 않는다.
ex ) 이진트리
3. O(n) Linear
입력값만큼 실행 시간과 비례하는 알고리즘이다. 선형 탐색 알고리즘 이라고도 한다.
ex ) for문
4. O(n log₂ n) Linear-Logarithmic
데이터가 늘어날수록 처리 시간이 log배만큼 더 늘어나는 알고리즘이다. 효율이 좋은 정렬 알고리즘들은 거의 여기에 해당ex ) 퀵정렬, 합병정렬
5. O(
데이터가 많아지면 처리 시간이 기하급수적으로 늘어나는 알고리즘.
ex ) 이중for문, 삽입정렬, 버블정렬, 선택정렬
6. O(2ⁿ) Exponential
데이터량이 많으면 많을수록 처리 시간이 기하급수적으로 늘어나는 알고리즘.
ex ) 피보나치수열, 재귀의 역기능
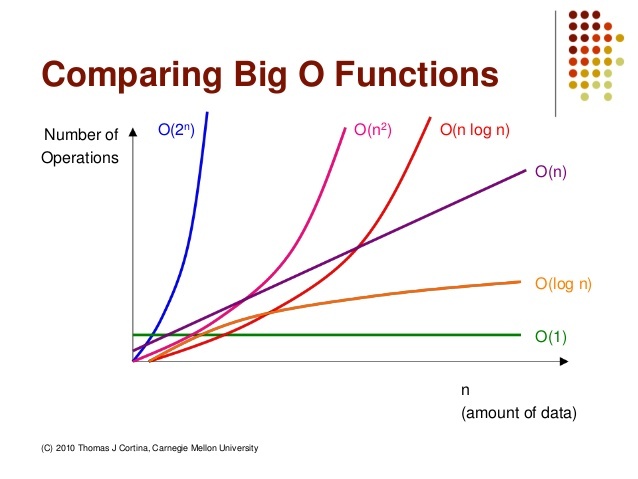
빅오표기법의 종류를 알았다면, 계산을 해보자.
빅오 표기법의 법칙
계수법칙 - 입력크기와 연관되지 않은 상수는 무시한다.
f(n)이 O(g(n))이면 k*f(n)은 O(g(n))
합의법칙 - 두개의 빅오를 더할 수 있다는 법칙. 합의 법칙 적용 후에 계수의 법칙을 적용해야 한다.
f(n)이 O(h(n)) 이고, g(n)이 O(p(n))이라면 f(n) + g(n)은 O(h(n) + p(n))
곱의법칙 - 두개의 빅오를 곱할 수 있다는 법칙. 곱의 법칙을 적용한 후에 계수 법칙을 적용해야 한다.
f(n)이 O(h(n)) 이고, g(n)이 O(p(n))이라면 f(n)g(n)은 O(h(n)p(n))
전이법칙 - 동일한 시간복잡도를 가진 알고리즘은 동일한 빅오 표기법을 가진다.
f(n)이 O(g(n))이고 g(n)이 O(h(n))이면 f(n)은 O(h(n))
다항법칙 - 시간복잡도가 동일한 다항 차수를 가진 알고리즘을 빅오로 표기하는 방법이다.
f(n)이 k차 다항식이면 f(n)은 O(n^k)
